教育王國
標題: DSE數學交流區 [打印本頁]
作者: 馬烏 時間: 25-5-19 18:25 標題: DSE數學交流區
坊間流傳2025年DSE數學難過2023年,我看了一下真題,感覺還是2023年的難度大一些。
感覺2024年的難度確實低於2023年和2025年 。
我個人覺得近三年難度排名是:2023>2025>2024。
歡迎交流。
作者: 馬烏 時間: 25-5-19 18:34
據說2026年DSE數學考試範圍排除極坐標,十六進制,函數定義域,跑道形軌跡等。
感覺這個十六進制確實沒啥意思,不過極坐標和函數定義域還是蠻重要的,不知何故排除?
作者: 馬烏 時間: 25-5-23 07:48
本帖最後由 馬烏 於 25-5-23 07:49 編輯
https://www.hk01.com/%E7%A4%BE%E ... D%E8%A9%95%E8%AB%96
2025年DSE數學mc34題,這麼明顯的題目錯誤,被多人指出,考評局還在硬撐。命題人水平低劣或者粗心大意。
這道題兩個函數圖像甚至可以有三個交點,加上同x軸一共可以有4個交點。
作者: 馬烏 時間: 25-6-24 11:38
本帖最後由 馬烏 於 25-6-24 11:53 編輯
網傳的內地初中升高中數學壓軸題。
作者: 馬烏 時間: 25-6-24 11:42
回覆 馬烏 的帖子
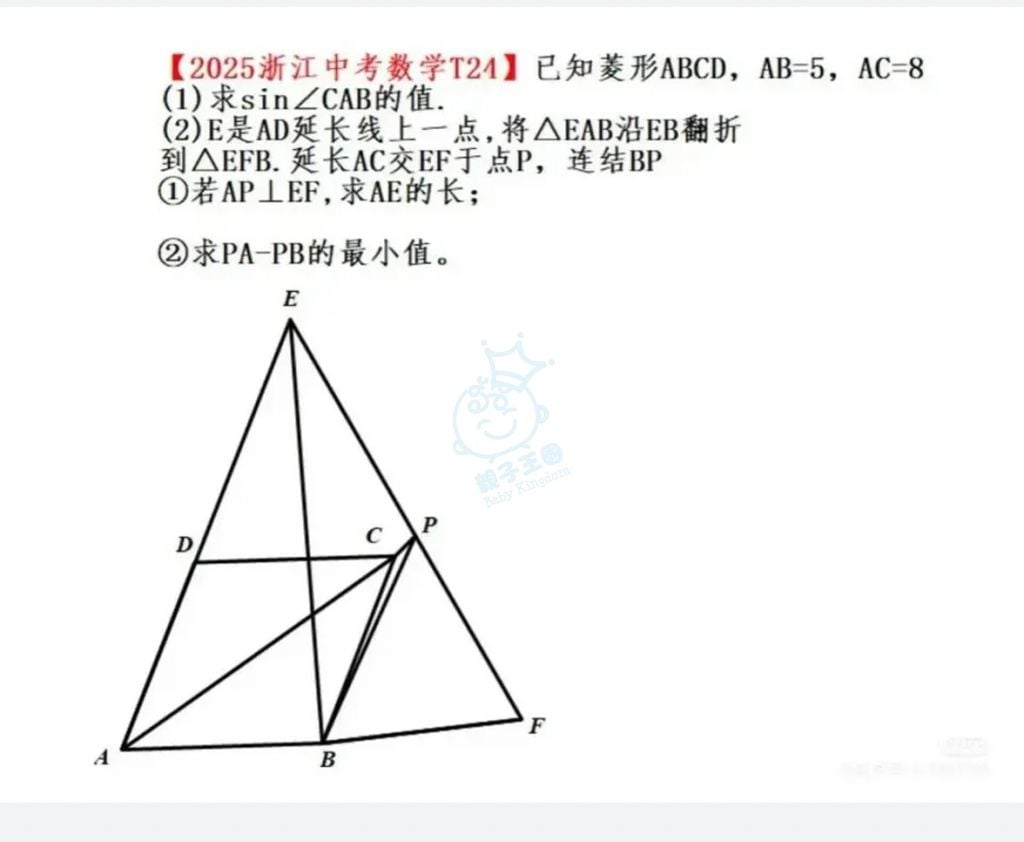
作者: 馬烏 時間: 25-6-24 11:52
馬烏 發表於 25-6-24 11:42 
回覆 馬烏 的帖子
作者: 2jkidsfather 時間: 25-6-26 13:32
本帖最後由 2jkidsfather 於 25-6-26 13:34 編輯
馬烏 發表於 25-6-24 11:42 
回覆 馬烏 的帖子
(1) sin ÐCAB = 3/5
(2)
(i) AE = 11
(ii) (PA-PB) 最小整數值是 6
除咗唔想人升高中,諗唔通出咁嘅數有乜意義。
作者: 馬烏 時間: 25-6-26 17:01
本帖最後由 馬烏 於 25-6-26 19:41 編輯
2jkidsfather 發表於 25-6-26 13:32 
(1) sin ÐCAB = 3/5
(2)
(i) AE = 11
前兩問做對 ,第三問沒做對,第三問也是最難的。
,第三問沒做對,第三問也是最難的。
浙江省的題目不是最難,據說江蘇省的題目經常讓考生想暴打出題人。
作者: 2jkidsfather 時間: 25-6-26 18:02
馬烏 發表於 25-6-26 17:01 
前兩問做對,第三問沒做對,第三問也是最難的。
浙江省的題目不是最難,據說江蘇省的題目經常讓學生 ...
作者: 馬烏 時間: 25-6-26 18:36
本帖最後由 馬烏 於 25-6-26 18:38 編輯
2jkidsfather 發表於 25-6-26 18:02 
你是有標準答案,定只是自己計算的答案?
標準答案還沒有出來,網上有一些人討論,最後一問有爭議。
6應該不對。如果P點和C點重合,這個最小值會是3。
如果把PA-PB用代數式表達出來,再求極值,會得出一個無理數,會小於3。這裡輸入法打不出來根號,我看看怎麼發上來這個參考答案。
我計過,感覺第一問比較簡單,第二問有點難度,但是也有方便的解法,第三問,有較大難度。
作者: 馬烏 時間: 25-6-26 18:51
本帖最後由 馬烏 於 25-6-26 18:52 編輯
PA-PB最小值: (3√39-4)/5
作者: 馬烏 時間: 25-6-26 19:17
需關注第三問,不能用第二問AP⊥EF這個約束條件。
第三問沒有垂直這個約束條件,P是個動點,第二問正好在垂直的位置,第三問則未知,這正是第三問的難點。
作者: gracelam 時間: 25-6-26 20:02
馬烏 發表於 25-6-24 11:52 
很多網友認為該題難度超DSE壓軸題。
DSE壓軸題應該唔會咁出。

作者: 馬烏 時間: 25-6-26 20:10
gracelam 發表於 25-6-26 20:02 
DSE壓軸題應該唔會咁出。
作者: LeeCC 時間: 25-6-26 21:15
馬烏 發表於 25-6-26 17:01 
前兩問做對,第三問沒做對,第三問也是最難的。
浙江省的題目不是最難,據說江蘇省的題目經常讓考生 ...
高考試卷題目每個省不同?
作者: 馬烏 時間: 25-6-26 21:29
本帖最後由 馬烏 於 25-6-26 21:30 編輯
LeeCC 發表於 25-6-26 21:15 
高考試卷題目每個省不同?
上面那道題是內地中考卷,內地初中升高中也是大考,中考卷每個省都不同。
高考是有些省份考卷相同,有些不同,現在是總共有八套試卷。
很多年以前的高考是全國一套卷。
作者: LeeCC 時間: 25-6-26 23:00
馬烏 發表於 25-6-26 21:29 
上面那道題是內地中考卷,內地初中升高中也是大考,中考卷每個省都不同。
高考是有些省份考卷相同,有些 ...
原來如此
咁8套卷程度一樣嗎?
作者: 馬烏 時間: 25-6-27 07:24
本帖最後由 馬烏 於 25-6-27 07:25 編輯
LeeCC 發表於 25-6-26 23:00 
原來如此
咁8套卷程度一樣嗎?
難度和考試範圍都不一樣。內地太大了,不同省份的教育水平有差別,城市和鄉村也有差別。
作者: LeeCC 時間: 25-6-27 08:37
馬烏 發表於 25-6-27 07:24 
難度和考試範圍都不一樣。內地太大了,不同省份的教育水平有差別,城市和鄉村也有差別。
...
明白
即係就算同分,山區和北京狀元的水平都不同?
作者: 馬烏 時間: 25-6-27 12:02
本帖最後由 馬烏 於 25-6-27 12:03 編輯
LeeCC 發表於 25-6-27 08:37 
明白
即係就算同分,山區和北京狀元的水平都不同?
肯定是這樣。這種情況古來有之,明代有名的南北榜案就是先例。區分難度就是為了照顧教育水平落後的地區。
下面這個著名的故事摘自維基百科。
南北榜案又稱「春夏榜案」。是發生在明朝洪武三十年(1397年)丁丑科會試。此次考試特別之處在於北方考生全數落榜,引發一時轟動。
事由
洪武三十年(1397年),翰林學士劉三吾、王府紀善白信蹈主持丁丑科殿試,後發榜,福建閩縣人陳䢿為第一,是為春榜,上榜者竟無一人出自北方,北平地區僅有一人[1]。諸多考生認為劉三吾為南方人,照顧其鄉親。朱元璋得知後大怒,命侍讀張信、侍講戴彝、右贊善王俊華、司直郎張謙、司經局校書嚴叔載、正字董貫、王府長史黃章、紀善周衡和蕭揖等人閱卷。後張信說劉三吾判卷無錯屬實。有人上告說劉三吾暗囑張信等人故意以陋卷進呈。朱元璋知道後更怒,指大部份官員是胡黨或藍黨,將張信與白信蹈等二十餘人淩遲處死,命劉三吾戍邊。劉諤、宋琮等人也遭遣戍,僅戴彝、尹昌隆免罪[2]。
後明太祖親自主持殿試,再選六十一名進士,都為北方人[3]。當時所謂「南北榜」或「春夏榜」[4][5]。
結果
南北榜案的結果導致自明仁宗時期起開始實行南北分卷。
作者: ok_ko 時間: 25-6-27 16:07
本帖最後由 ok_ko 於 25-6-27 16:27 編輯
馬烏 發表於 25-6-26 17:01 
前兩問做對,第三問沒做對,第三問也是最難的。
浙江省的題目不是最難,據說江蘇省的題目經常讓考生 ...
關於2.1
我不知道在高考或者中考是否只是比個答案就可以。假如只是比個答案,又假如你夠清醒。要做到AP垂直EF,P與C必然重叠。這樣AE必然是10。可能我算錯。爲什麽是11?
另外PA - PB是一個上升函數(在P與C重叠之後)。最小值為3(發生在 P與C 重叠時),最大值逼近4。
作者: 馬烏 時間: 25-6-27 16:51
本帖最後由 馬烏 於 25-6-27 16:53 編輯
ok_ko 發表於 25-6-27 16:07 
關於2.1我不知道在高考或者中考是否只是比個答案就可以。假如只是比個答案,又假如你夠清醒。要做到AP垂直 ...
長答題要有解題步驟,答對的步驟都算分,和DSE一樣。如果是填空題和選擇題,就只要答案就行。
2.1,AE是11,垂直時不會重疊。P,C有重疊這種情況,但此時AP,EF不垂直。你可仔細看看,連接BD,三角形BDE是等腰三角形,因此DE=BD=6,AE=6+5=11。解法有很多,找出這個等腰三角形方法最簡便。
第三問有難度,這裡文字三言兩語不大容易說清楚,上面聊的內容有思路,有興趣可以再琢磨琢磨,再看看怎麼探討。
作者: ok_ko 時間: 25-6-27 17:11
馬烏 發表於 25-6-27 16:51 
長答題要有解題步驟,答對的步驟都算分,和DSE一樣。如果是填空題和選擇題,就只要答案就行。
2.1,AE是1 ...
作者: 馬烏 時間: 25-6-27 18:06
ok_ko 發表於 25-6-27 17:11 
很好!
作者: 馬烏 時間: 25-6-27 18:25
本帖最後由 馬烏 於 25-6-27 18:51 編輯
轉帖一個解說供感興趣的網友參考。我也是剛剛看到。
难破天际的2025中考数学卷,到底难在哪里?
鱼圈教研团,2025年06月
今年浙江中考数学刚考完,不少浙江家长、老师和学生都围着一道题吵翻了。一开始是因为试卷原题还未公布,对于题目中的条件是“射线”还是“延长线”谁也不敢下定论,而这几个字的区别会决定这道题目的难度是上天还是入地。如今答案已经揭晓,原题说的是:点P在射线AC上。这意味着,这题的得分率大概率不会太高……那么,从这道压轴题来看出题方向,家长能有什么思路呢?是不是真得学点奥数竞赛啥的?我们今天就简单聊聊这道题背后的“难”,以及应对的思路。
这是2025年浙江中考数学压轴题第三问的网传官方解析,解法1和解法2都是几何+代数思路,解法1更偏代数,解法2更偏几何。
ps:本题还有其他解法,有兴趣可以自行搜索,我们暂且先按官方答案来解读。
从解析可以看出,这道题在思维深度和几何技巧方面的要求都非常高。1. 需要具备扎实的几何模型能力。
这题用了不少隐藏几何模型、定理和性质。比如:解法 1通过一系列代数转化,将PA-PB表达式转成与PB有关的代数式。然后利用“点到线段的最短距离是垂线段”的几何性质,把代数问题转为求B到AD的垂距。解法 2构造了“等距离”点,通过三角形边角关系推导出“等腰+角最大=对边最小”,结合垂距进一步解题。这里的难点在于,考生如何通过添加辅助线把距离最短这个概念和提问联系起来。它不像普通的几何辅助线,添加后就一目了然,而是得一步步推导后才能确定答题方向。如果此前没有过这种构造经验的学生,很难在考场上想到这一层。2. 需要建立代数-几何混合思维,思考链路很长对初中学生来说,想要把几何问题变成代数表达,对他们来说挑战非常大。
我们以解法1为例。
式子里出现PB、PO两个未知数,而初中并没有学过单调性判断最值,所以需要孩子能自行推导出下面的逻辑:PA-PB最小,就要让PB-PO最大;PB-PO最大不好求,就要先通过勾股定理得到以下代数式:从而转化成有关PB大小的代数式而PB最小,等于点B到EF线段的距离(也就是图上的垂直距离),得到PB最短距离=25/4最后代入原算式,求出答案。
整个过程依赖大量前置条件,任一环节失误,答题链条就崩了。以上这些内容,你说超纲了嘛?那肯定没有,确实都是初中的知识,尤其是距离最短这一几何学习重点。但许多孩子想不到,因为这些方法有点反常规,初中课堂教学中极少系统讲授,属于竞赛训练或深度选拔题的常用技法。说白了,就是大家都觉得中考不可能考得那么深,尤其是对比去年中考试卷的压轴题,今年的思维拔高了好几度。
作者: 馬烏 時間: 25-6-28 10:03
本帖最後由 馬烏 於 25-6-28 10:03 編輯
接下來想聊聊DSE數學的坐標幾何。
看過最近幾年的DSE數學真題,感覺坐標幾個是DSE數學的重中之重,如果想摘星,坐標幾何不過關幾乎不可能,最後一道12分的大題,幾乎每年都是坐標幾何題。
此外,section B部分坐標幾何至少還有一題,兩題合計占約20分,加上A部分及MC卷,坐標幾何總體占分有40分左右。
以2025年為例,長答題18,19題都是坐標幾何,兩題分別占分9,12,只此兩題已占21分。
作者: barque 時間: 25-6-28 11:06
難得身為家長還記得高中的數學,有次孩子問我有關quadratic equation的問題,我叫佢自己睇YouTube. 因為真是不記得了

作者: 馬烏 時間: 25-6-28 11:49
barque 發表於 25-6-28 11:06 
難得身為家長還記得高中的數學,有次孩子問我有關quadratic equation的問題,我叫佢自己睇YouTube. 因為真 ...
作者: 馬烏 時間: 25-6-28 13:26
一道有意思的數學題。solve equation:
(x+3)(x+5)(x+7)(x+9)=9
感覺能解出來的小朋友,應該數學很不錯。
作者: 流浪地球 時間: 25-6-28 16:29
本帖最後由 流浪地球 於 25-6-28 16:33 編輯
馬烏 發表於 25-6-28 13:26 
一道有意思的數學題。solve equation:
(x+3)(x+5)(x+7)(x+9)=9
方程的解為:
\
\boxed{x=-6,\quad x=-6+\sqrt{10},\quad x=-6-\sqrt{10}}
\]
注意:\(x = -6\) 是重根(重數為 2),但在解集中列出一次即可。
\boxed{x=-6} \quad \boxed{x=-6+\sqrt{10}} \quad \boxed{x=-6-\sqrt{10}}
「堞仙」用咗80 秒和去解題,不知是否正確?
作者: 馬烏 時間: 25-6-28 18:03
流浪地球 發表於 25-6-28 16:29 
方程的解為:
\
\boxed{x=-6,\quad x=-6+\sqrt{10},\quad x=-6-\sqrt{10}}
作者: 流浪地球 時間: 25-6-28 21:09
馬烏 發表於 25-6-28 18:03 
解對了,趕緊請教,蝶仙是啥?
作者: 馬烏 時間: 25-6-28 21:40
流浪地球 發表於 25-6-28 21:09 
堞仙咪DeepSeek 囉😀

作者: 流浪地球 時間: 25-6-28 21:58
馬烏 發表於 25-6-28 21:40 
原來是“請槍”,現在宣佈成績作廢
作者: 馬烏 時間: 25-6-28 22:45
流浪地球 發表於 25-6-28 21:58 
成績能代表甚麽呢。數學呢啲嘢,我自己親身經歴,從小學一年級到初中,數學科從未及格過,年年都係成績表上 ...

作者: 流浪地球 時間: 25-6-28 23:01
馬烏 發表於 25-6-28 22:45 
小一數學都能不及格?可媲美錢鐘書啦
作者: 馬烏 時間: 25-6-28 23:24
流浪地球 發表於 25-6-28 23:01 
我研究咗好耐,原來真正嘅天才,一般數學成績都是零雞蛋嘅。


項目可命名: AI免犯錯得雞蛋之天才解決方案
作者: 流浪地球 時間: 25-6-29 13:57
馬烏 發表於 25-6-27 18:25 
轉帖一個解說供感興趣的網友參考。我也是剛剛看到。
难破天际的2025中考数学卷,到底难在哪里?
(1)3/5
(2)AE= 11
(3) 最小整數值是 -5
DeepSeek 在沒有圖稿下 推想用時508 秒 得到答案。
作者: 馬烏 時間: 25-6-29 14:05
流浪地球 發表於 25-6-29 13:57 
DeepSeek 最終答案
(1)3/5

第三問Deep seek顯然沒做對。
作者: 流浪地球 時間: 25-6-29 14:33
本帖最後由 流浪地球 於 25-6-29 14:37 編輯
馬烏 發表於 25-6-29 14:05 
那全體數學老師都松了一口氣,不用擔心被人工智能砸爛飯碗了。
第三問Deep seek顯然沒做對。
...
最小絕對值是3 。
作者: 流浪地球 時間: 25-6-29 14:49
流浪地球 發表於 25-6-29 14:33 
最小絕對值是3 。
人生時間有限,值唔值得花時間去研究?我只係知道去街市買餸,唔會用到sin 同 cos。
作者: 馬烏 時間: 25-6-29 14:59
流浪地球 發表於 25-6-29 14:33 
最小絕對值是3 。
按后面流出的真题说明和解答,应该还是小于3的那个无理数。
作者: 馬烏 時間: 25-6-29 15:03
流浪地球 發表於 25-6-29 14:49 
數學真係多花様,分咩叫極值,無理數,絕對值,虛數…..大多花款。
人生時間有限,值唔值得花時間去研究? ...
現在算盤也免了。
作者: 流浪地球 時間: 25-6-29 15:13
馬烏 發表於 25-6-29 14:59 
如果取最小整数应该是3。
按后面流出的真题说明和解答,应该还是小于3的那个无理数。
第二次我要求絕對最小值。得出是3 DeepSeek 加多句(可無限接近3 )。
作者: 流浪地球 時間: 25-6-29 15:44
馬烏 發表於 25-6-29 15:03 
所以以前做生意的人讀書,讀個小學和打算盤就可以了。
現在算盤也免了。
作者: 流浪地球 時間: 25-6-29 16:02
馬烏 發表於 25-6-28 21:40 
原來是“請槍”,現在宣佈成績作廢
作者: 馬烏 時間: 25-6-29 17:22
流浪地球 發表於 25-6-29 15:44 
打算盤,我讀小學課程是有教的。我苦思點解我小學數學成績咁差勁,之後我找到一個不是理由的理由。當年我唸 ...
香港学算盘到什么年代?算盘这玩意确实已经被淘汰了,以后只能当文物展览。
作者: 馬烏 時間: 25-6-29 17:29
本帖最後由 馬烏 於 25-6-29 17:31 編輯
流浪地球 發表於 25-6-29 16:02 
“請槍” 不就是=出術。我唔講原由,你唔知曉真相,成績就不會作廢。過咗海就成神仙。 ...
我學生時代,平日考試好多作弊的,被捉到的都比較笨拙,90%是捉不到的。
作弊最主要原因,太部分是怕分數低回家挨打。
作者: 馬烏 時間: 25-6-29 17:39
流浪地球 發表於 25-6-29 15:44 
打算盤,我讀小學課程是有教的。我苦思點解我小學數學成績咁差勁,之後我找到一個不是理由的理由。當年我唸 ...
中國的古代數學沒有代數。有九章算術,但是沒有九章數學。
作者: 流浪地球 時間: 25-6-29 18:24
馬烏 發表於 25-6-29 17:39 
中國古代沒有數學,只有算術。嚴格來說只有代數出現後才能算數學。
中國的古代數學沒有代數。有九章算術, ...
一律有個代字,都係表達不是「正」貨。本源。本質。本色。如成語「李代桃僵。」
如此推論,古代稱算術先係玄門正宗。
話時話,古代同現代,都有個代字,諗吓諗吓,時間同空間就係咁劃分。確實幾有趣。
作者: 馬烏 時間: 25-6-30 08:06
本帖最後由 馬烏 於 25-6-30 08:10 編輯
流浪地球 發表於 25-6-29 18:24 
嗱,照字面字義睇,咁就有啲表面証據,可以話我講果的不是理由。多少都有啲根據。「代數」出現之後才改稱數 ...
正貨,本源,正宗,不一定好,不一定高級,往往很low。
代就上檔次了,新的代替舊的,好的代替壞的,新陳代謝好不好?沒有代謝就要命啊
手機代替bp機,汽車代替牛車馬車,代往往代表更高級。
以前穿樹皮獸皮,現在代之各種各樣衣服。
代數比算術高級,那是無疑的。靠算術,我們恐怕沒法這樣用手機溝通
算術的天花板是算盤,數學出現了計算機,人工智能,現在還不知道天花板在哪裡呢
作者: 流浪地球 時間: 25-6-30 11:10
馬烏 發表於 25-6-30 08:06 
正貨,本源,正宗,不一定好,不一定高級,往往很low。
代就上檔次了,新的代替舊的,好的代替壞的,新陳 ...
「 末代皇帝」溥儀 落點係個末字,最後的意思。
小學算術有課程是教 雞兔同籠 。這個算不算是代數?
算術,代數。在玄學界中有個名詞叫 術數。先有術才有數。又或者可以說大家係相輔相成。
算術天花板係在「道」。有道無術,術尚可求。有術無道止於術。
作者: 馬烏 時間: 25-6-30 13:14
本帖最後由 馬烏 於 25-6-30 13:16 編輯
流浪地球 發表於 25-6-30 11:10 
嗱嗱,你就唔好忽悠我叻。代字不是代表好與壞,新與舊,亦同檔次無𨶹。「-代不如一代」重點係在不 ...

[size=18.6667px]
道不明,說不清。道是一筆糊塗賬。
道可道非常道。標點符號不知道該點哪裡。道之為物,唯恍唯惚。忽兮恍兮,其中有象;恍兮忽兮,其中有物。窈兮冥兮,其中有精;其精甚真,其中有信。
你看,就是車轱轆話來回說,道才是真忽悠啊
作者: 流浪地球 時間: 25-6-30 14:40
馬烏 發表於 25-6-30 13:14 
可別被道忽悠了。
道不明,說不清。道是一筆糊塗賬。
作者: 馬烏 時間: 25-6-30 15:25
流浪地球 發表於 25-6-30 14:40 
冇所謂啦,我都係胡說八道,尋找樂趣而已。

作者: 2jkidsfather 時間: 25-6-30 17:40
本帖最後由 2jkidsfather 於 25-6-30 17:44 編輯
馬烏 發表於 25-6-24 11:42 
回覆 馬烏 的帖子
上面題目寫明
「延長AC(相)交EF於點P」
即是 長度 PA 永遠 > AC
所謂標準答案的步驟根本當了 PA<=AC
PA<=AC,咁點P如何在EF?
條件不符題目,咁都收貨?
作者: 2jkidsfather 時間: 25-6-30 18:06
馬烏 發表於 25-6-26 19:17 
需關注第三問,不能用第二問AP⊥EF這個約束條件。
第三問沒有垂直這個約束條件,P是個動點,第二問正好在 ...
現在是兩條不動線相交出P點。
Locus(即是「動點」) 係香港係高中課程。
初中升高中的考試會有「動點」?
作者: 馬烏 時間: 25-6-30 18:14
本帖最後由 馬烏 於 25-6-30 18:16 編輯
2jkidsfather 發表於 25-6-30 18:06 
「動點」...是否想多了?
現在是兩條不動線相交出P點。
前面回復有貼出官方真題和解答,可參考。
第一次貼出的題是網友憑回憶發佈的,描述有點缺陷,後面真題有說明AC是射線,那就沒有問題了。
內地數學程度同級相比,比香港深一些,初中出現動點是可以的,不超考試範圍。
如曲線方程,內地要學橢圓和雙曲線,香港也是不學的。考試範圍略有差異。
作者: cherrieshum 時間: 25-7-3 15:19
回覆 馬烏 的帖子
多謝分享資訊,阿女最喜歡M2及數學兩科
| 歡迎光臨 教育王國 (/) |
Powered by Discuz! X1.5 |

 ,第三問沒做對,第三問也是最難的。
,第三問沒做對,第三問也是最難的。




















