教育王國

標題: Maths question - need help! [打印本頁]

作者: vanlam8 時間: 20-12-4 01:42 標題: Maths question - need help!

Does anyone know how to calculate this? thanks a lot!

圖片附件: 16070173203833642073755705114650.jpg (20-12-4 01:42, 319.35 KB) / 下載次數 21
/forum.php?mod=attachment&aid=MzU2Njk4fDhlNzAxMzcxfDE3NTM5OTU3MjN8MA%3D%3D

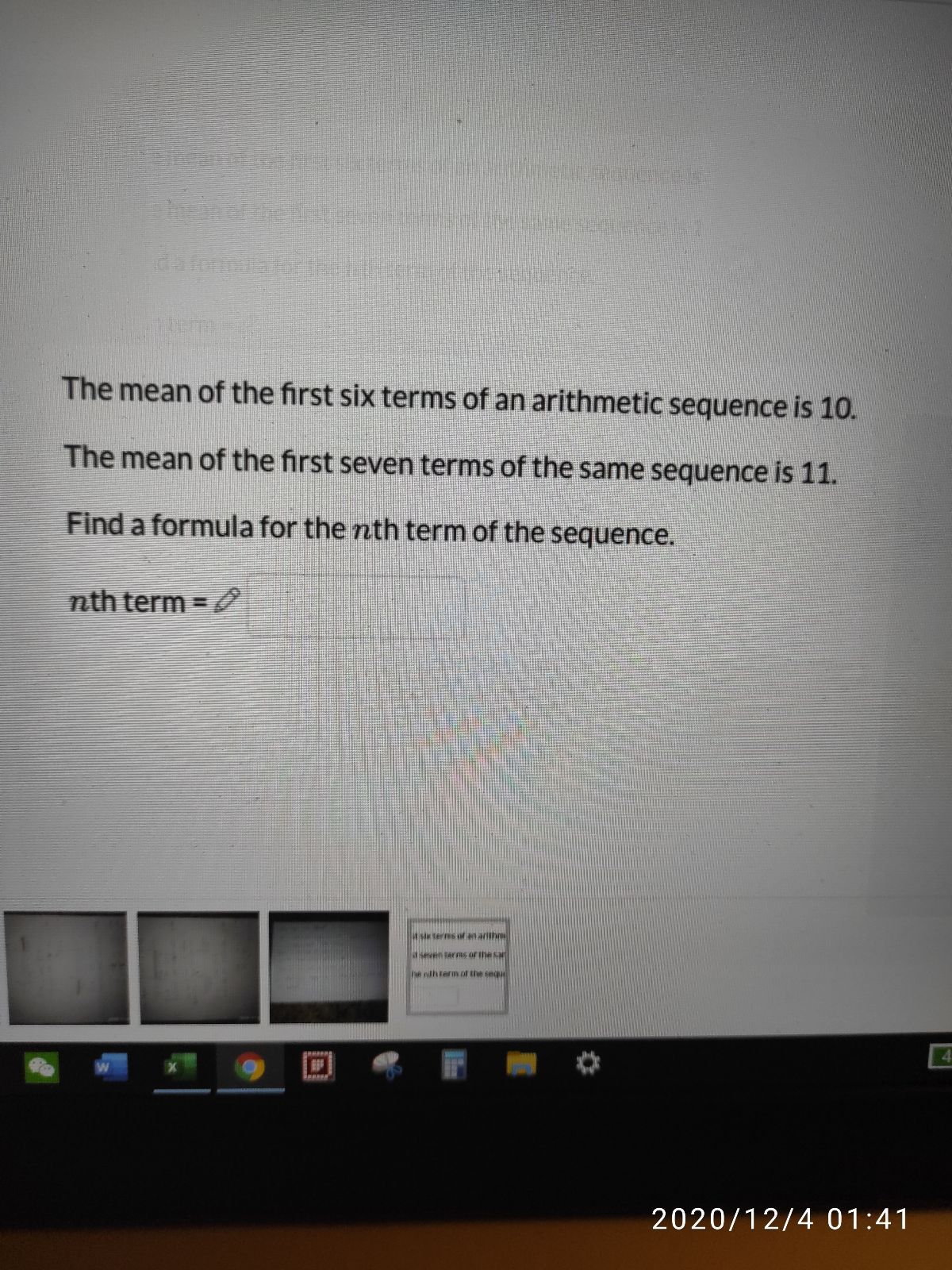
作者: cafeva 時間: 20-12-5 16:18

vanlam8 發表於 20-12-4 01:42
Does anyone know how to calculate this? thanks a lot!

2n+3right?

作者: djf 時間: 20-12-7 14:34

回覆 cafeva 的帖子

S(n)=n[2a+(n-1)d]/2
6(2a+5d)/2 = 60 ----- (i)
7(2a + 6d)/2 = 77 ----- (ii)

d = 2, a = 5

T(n) = 10 + 2(n-1)
T(n) = 3 + 2n

作者: 小鹿揀學校 時間: 21-2-16 09:20

本帖最後由小鹿揀學校於 21-2-16 09:24 編輯

n(7) = 11X7 - 10X6 = 17

11 = (a + n(7)) / 2 , a=5

n(7)  = 17 = a + 6d , d = 2

n(n) = 5 + (n-1)2  = 3 + 2n

作者: YmOra 時間: 21-2-16 10:54

已知：
頭６項等差級數之平均值為１０，亦代表這堆數之"中位數"為１０；
頭７項等差級數之平均值為１１，亦代表這堆數之"中位數"為１１，
又頭７項等差級數之中位數會排列响第４項之值，即"項４"等於１１。

由於，相鄰"項"之"中位數"相差０.５ｄ。
即：
　　０.５ｄ＝１１-１０＝１
　∴　　ｄ＝２

　　ｎ(４)＝１１＝ａ＋（４-１）２
　∴　ａ＝５

即：ｎ(ｎ)＝５＋（ｎ-１）２＝２ｎ＋３

作者: 小鹿揀學校 時間: 21-2-16 12:41

YmOra 發表於 21-2-16 10:54
已知：
頭６項等差級數之平均值為１０，亦代表這堆數之"中位數"為１０；
頭７項等差級數之平均值為１１，亦 ...

你咁做要花篇幅解釋, 個 marker 先明你做乜, 唔夠 efficient 又有扣 step分風險·…
n(7) = T(7) - T(6) = 11X7 - 10X6 = 17.... 簡單易明不須再作解釋.·⋯

大家切磋切磋, 並無他意

作者: YmOra 時間: 21-2-16 15:44

小鹿揀學校發表於 21-2-16 12:41
你咁做要花篇幅解釋, 個 marker 先明你做乜, 唔夠 efficient 又有扣 step分風險·…
n(7) = T(7) - T(6) = ...

我上面三句係讓ｊｍ們明白下面做緊乜而矣才咁長氣寫咁多，其實上面每樓層的人之計算方法都是正確的無任何問題，我只是想擴闊ｊｍ們的視嘢，豐富數學的認知而矣。我這方法係當年的數學老師响堂上額外教的方法，老師會強化我們計數的"數速"，目的係為應付主科數中的ＭＣ卷，老師話這類數如果係出响選擇題樹就要靠平時多豐富對數題的不同角度而進行的計算，因為要應付數學選擇題卷就必需練習"快計"的方法。其實，我會直接使用下方的公式計這題，現証明公式如下。

已知基本公式為：
　　　　　ａ1＋ａ1＋（ｎ-１）ｄ
Ｓｎ＝（————————————）ｎ
　　　　　　　　　２

所以：：
  Ｓｎ
———＝中位數（ｎ項）＝平均數（ｎ項）——＞當年有記嘅公式１
　ｎ

　　　　　　　　ｎ-1
　　　＝ａ1＋（———）ｄ
　　　　　　　　  ２

所以：：：
  Ｓｎ　　　　　　　　　　　　　  ｎ-1
———＝中位數（ｎ項）＝ａ1＋（———）ｄ———①
　ｎ　　　　　　　　　　　　　　  ２

Ｓｎ+1　　　　　　　　　　　　　　　ｎ
————＝中位數（ｎ+1項）＝ａ1＋（———）ｄ——— ②
　ｎ+1　　　　　　　　　　　　　　　  ２

② - ①得出公式：
中位數差＝平均數差＝０.５ｄ——＞當年有記嘅公式２

歡迎光臨教育王國 (/)