教育王國
標題: 请教數學題 [打印本頁]
作者: jilin1960 時間: 15-2-14 21:07 標題: 请教數學題
Thirty-two feet of fencing materials is used to enclose a garden that is a rectangluar region .if the numble of square feet in the region is f ,what is the largest possible value of f?
作者: jasonsuen 時間: 15-2-14 22:40
32/4 = 8
f = 8*8 = 64
square is a kind of rectangle.
作者: jilin1960 時間: 15-2-15 07:50
Thx.孩子以為rectangle 不可以是square.
作者: kenwong888 時間: 15-2-15 16:05
本帖最後由 kenwong888 於 15-2-15 16:06 編輯
jilin1960 發表於 15-2-14 21:07 
Thirty-two feet of fencing materials is used to enclose a garden that is a rectangluar region .if th ...
It is nothing dealing with rectangle or square?
What is the reason square is max area?
Formally we use differentiation to solve the problem:-
f= (16-x)x
df/dx = 16-2x
For local max, df/dx=0
so x=8
right???
作者: Unclejt 時間: 15-2-15 16:24
Completing the square:
(16-x)x = 64 - (64 - 16x + x^2) = 64 - (x - 8)^2 >= 64,
and equality holds when x = 8.
作者: kenwong888 時間: 15-2-15 21:20
Unclejt 發表於 15-2-15 16:24 
Completing the square:
(16-x)x = 64 - (64 - 16x + x^2) = 64 - (x - 8)^2 >= 64,
Let say if the total length is 31 right???
作者: fungsir 時間: 15-2-15 22:48
if it is a rectangle, the largest possible value of f should be 63.
作者: kenwong888 時間: 15-2-15 22:56
fungsir 發表於 15-2-15 22:48 
if it is a rectangle, the largest possible value of f should be 63.
f needs to be integer right?
Anyway...just kidding...
作者: Unclejt 時間: 15-2-15 22:58
回覆 kenwong888 的帖子
If the total length is A, then
(A/2 - x)x = A^2/16 - (A/4 - x)^2.
Maximum value = A^2/16, attended at x = A/4.
作者: dlee_ca 時間: 15-2-15 23:04 標題: 引用:32/4+=+8f+=+8*8+=+64square+is+a+kind+of+
本帖最後由 dlee_ca 於 15-2-15 23:08 編輯
原帖由 jasonsuen 於 15-02-14 發表
32/4 = 8
f = 8*8 = 64
square is a kind of rectangle.
Square is kind Rectangle. Interesting.

作者: kenwong888 時間: 15-2-15 23:33
Unclejt 發表於 15-2-15 22:58 
回覆 kenwong888 的帖子
If the total length is A, then
But I do think the student can easily classify the problem as finding local max or min right???
作者: 1234ats 時間: 15-2-16 10:03
本帖最後由 1234ats 於 15-2-16 12:47 編輯
Whether a square is a rectangle or not depends on the definition of these shapes.
My son’s primary school and textbook teach students that squares are not rectangles.
But if one defines a rectangle as a quadrilateral with equal opposite sides and all the four angles equal to 90 degrees, then squares should be considered as rectangles.
I would say both are correct but students should realize their differences.
In this maximum area problem, apparently square is rectangle. Otherwise the maximum area will be infinitesimally close to 64 but not equal to 64, which is an alien concept for those who have not learnt calculus.
作者: 1234ats 時間: 15-2-16 10:04
本帖最後由 1234ats 於 15-2-16 12:46 編輯
Kenwong888
I would expect anyone who can master quadratic equations should be able to instantly identify that X(16-X) is a quadratic expression. It is equal to -(X-0)(X-16).The minus sign shows this parabolic curve has a maxima. And this maxima vertex is located at X = (0+16)/2 = 8 [i.e. mid way between 0 & 16] because of the symmetrical nature of parabola. Thus one should be able to get maximum area 8x8=64 by heart. It is a few-second-problem.
But anyway, I think this problem is a bit too hard for primary students. It would be more suitable to post it in secondary school section.
作者: jasonsuen 時間: 15-2-17 01:57
講真,這是一道小學的數學題,但屬思考性題目,請用一個小學生能明白的方法吧,否則就是不切實際。
作者: kenwong888 時間: 15-2-17 07:41
1234ats 發表於 15-2-16 10:04 
Kenwong888
I would expect anyone who can master quadratic equations should be able to instantly ide ...
作者: laorenjia 時間: 15-2-17 15:59
本帖最後由 laorenjia 於 15-2-17 16:10 編輯
妻子話我頭腦簡單,channel 同細路仔差唔多,若我講數細路仔聽唔明,就冇人會講得個細路明。(其實係見氹我教阿女數,等佢唔駛出馬)
若果呢題係小學數,就咪鬼講乜嘢completing the square, 細路仔點會明?你同個細路講:正方形係矩形一種,若周界一樣,正方形就面積最大。唔駛嚴格證明,呢條題目32/4=8。8 x 8 就最大面積,叫細路試吓7 x 9,6 x 10...就知面積越嚟越細。反之9 x 7, 10 x 6... 亦然,搞掂。
作者: JustAParent 時間: 15-2-17 17:38 標題: 引用:+本帖最後由+laorenjia+於+15-2-17+16:10+
原帖由 laorenjia 於 15-02-17 發表
本帖最後由 laorenjia 於 15-2-17 16:10 編輯
妻子話我頭腦簡單,channel 同細路仔差唔多,若我講數細路 ...

作者: kenwong888 時間: 15-2-17 23:56
laorenjia 發表於 15-2-17 15:59 
妻子話我頭腦簡單,channel 同細路仔差唔多,若我講數細路仔聽唔明,就冇人會講得個細路明。(其實係見氹我 ...
Maybe modern people need more training!
作者: laorenjia 時間: 15-2-18 10:47
kenwong888 發表於 15-2-17 23:56 
I really do not understand your logic!
Maybe modern people need more training!
作者: 王家爸爸 時間: 15-2-18 13:17
1234ats 發表於 15-2-16 10:03 
Whether a square is a rectangle or not depends on the definition of these shapes.
My son’s primary ...
What is a square? A square is also a parallelogram with four right angles.
Therefore, a square is a special case of rectangle which has all sides of the same length.
作者: laorenjia 時間: 15-2-18 16:05
本帖最後由 laorenjia 於 15-2-18 16:06 編輯
kenwong888 發表於 15-2-17 23:56 
I really do not understand your logic!
Maybe modern people need more training!
抵唔住頸,試多次:
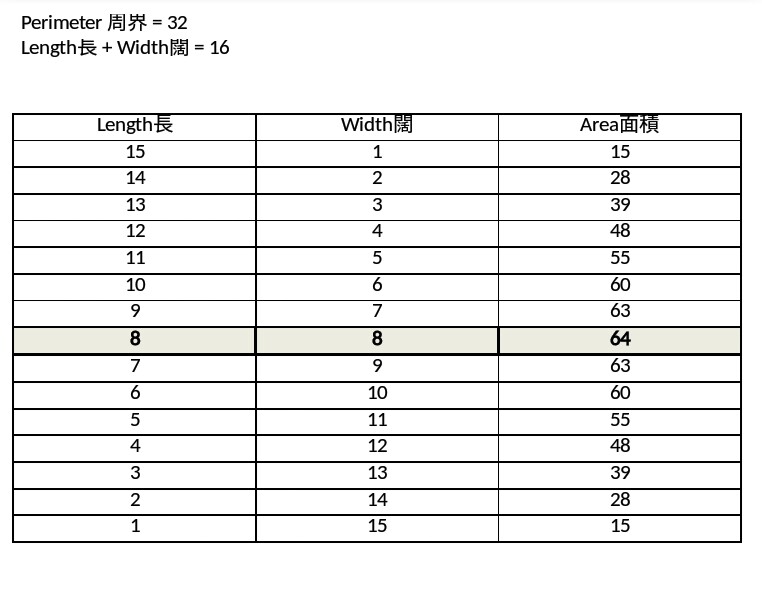
周界32,若是正方形,邊長就等於32/4=8。面積就係8x8=64。跟手就證明呢個係最大面積,若果圖形係長方形,長加濶等於32/2=16。簡單啲用整數諗,長同闊嘅組合有9x7, 10x6, 11x5, ..., 14x2, 15x1, 面積一路細落去,所以正方形就最大。
作者: kenwong888 時間: 15-2-18 16:24
laorenjia 發表於 15-2-18 16:05 
抵唔住頸,試多次:
周界32,若是正方形,邊長就等於32/4=8。面積就係8x8=64。跟手就證明呢個係最大面積, ...
作者: kenwong888 時間: 15-2-18 16:26
laorenjia 發表於 15-2-18 10:47 
都話妻子氹我啦。唔用代數或微積分講得你明,唯有另請高明。
作者: laorenjia 時間: 15-2-18 16:37
本帖最後由 laorenjia 於 15-2-18 16:38 編輯
The integer answer is the result, not the requirement. I only used integers to show the change in the area. It is not mathematical induction. You've confused yourself with all the techniques in high school maths. I thought we were talking how to explain to a primary school kid.
作者: kenwong888 時間: 15-2-18 22:26
laorenjia 發表於 15-2-18 16:37 
The integer answer is the result, not the requirement. I only used integers to show the change in th ...
Seems your logic is assuming something which is not stated explicitly, a very common mistake to take all for granted right???
作者: compsognathus 時間: 15-2-19 00:10
As an S1 student in SIS, I would like to try to tackle this problem.
Firstly, there is the problem of whether the child's textbooks consider a square a rectangle. I will now explain why a square is a rectangle.
-By definition, a quadrilateral is a polygon with four sides. Therefore, one can infer:
-A parallelogram is a quadrilateral with opposite sides parallel. Therefore, one can infer:
-A rectangle is a parallelogram with four right angles. Therefore, one can infer:
-A square is a rectangle with four congruent sides. Therefore, a square is a rectangle.
Secondly, there is the problem of whether one can only use integers. If one can only use integers, you can simply utilize guess and check to find the answer, even if a square is not considered a rectangle by the child's textbooks. If all real numbers are permitted and a square is not a rectangle, then one starts dealing with calculus. The value of f would then be “infinitesimally close to 64 square feet”.
Completing the square has assumed the rectangle was a square. If one assumes the rectangle is a square, the method holds in theory, but there is a much easier method which has been covered in the second post by jasonsuen. Though, a primary school student may not be able to prove that the square has the greatest area for any quadrilateral with perimeter x.
Therefore, I recommend the guess and check method for a primary student to approach this question. Guess and check is also a learning experience in this case, as students will discover that the square is the quadrilateral that has the largest area for any given perimeter x.
作者: c1234 時間: 15-2-19 23:38
回覆 laorenjia 的帖子
真是好方法
作者: laorenjia 時間: 15-2-20 03:14
本帖最後由 laorenjia 於 15-2-20 10:03 編輯
kenwong888 發表於 15-2-18 22:26 
Then you need to show the logic is also correct for real number right???
Seems your logic is assumin ...
A third and the final attempt.
Actually, the proof is vigorous enough as the function x(16-x) is a continuous function over the domain (0, 16). But this is for you only as you seem to be still obseesed with whether the solution is vigorous enough with the question on real numbers which a normal primary kid will not concern himself with.
作者: kenwong888 時間: 15-2-20 08:06
laorenjia 發表於 15-2-20 03:14 
A third and the final attempt.
Amazing!!!
作者: laorenjia 時間: 15-2-20 09:58
kenwong888 發表於 15-2-20 08:06 
Well, you now demand the primary student to have the concept of function, continuity, singularity, a ...
作者: kenwong888 時間: 15-2-20 10:02
本帖最後由 kenwong888 於 15-2-20 10:04 編輯
laorenjia 發表於 15-2-20 09:58 
Stupid me. I left out an explanation. Now added.
I think good primary students know real number right???
Fractional and decimal number is real number right???
Rational number is real number they need to grasp right???
作者: laorenjia 時間: 15-2-20 11:10
kenwong888 發表於 15-2-20 10:02 
I think good primary students know real number right???
Fractional and decimal number is real numbe ...
作者: kenwong888 時間: 15-2-20 14:01
laorenjia 發表於 15-2-20 11:10 
In HK the concept of real numbers is formally introduced when students learn about complex numbers b ...
OK no real number!!!
You should know definition of rational number right???
Kind of representation of " M / N " is rational number M & N integer right???
Don't scare me if primary student don't know fractional number!!!
作者: laorenjia 時間: 15-2-20 14:36
本帖最後由 laorenjia 於 15-2-20 14:45 編輯
kenwong888 發表於 15-2-20 14:01 
OMG!
OK no real number!!!
You should know definition of rational number right???
Mankind has been using real numbers since day one, but the concept of real numbers was not known to us until after the great Pythagoras. And why all a sudden a kid will understand what real numbers mean if he knows what a fractional number is?
作者: lamyeelok 時間: 15-2-20 15:11
提示: 作者被禁止或刪除 內容自動屏蔽
作者: kenwong888 時間: 15-2-20 15:36
本帖最後由 kenwong888 於 15-2-20 15:36 編輯
laorenjia 發表於 15-2-20 14:36 
Mankind has been using real numbers since day one, but the concept of real numbers was not known to ...
I am now saying no need to understand real number!!!
But they still know fractional number right???
Seems you have mixed up a lot of concept but just focusing on the "name" or "form"!!!
What is substantial is that they should know there exists fractional numbers but integers!!!
Should they consider the possible answers not limited to integer???
作者: kenwong888 時間: 15-2-20 15:37
lamyeelok 發表於 15-2-20 15:11 
分清楚real numbers 同natural numbers
作者: laorenjia 時間: 15-2-22 11:54
本帖最後由 laorenjia 於 15-2-22 12:31 編輯
lamyeelok 發表於 15-2-20 15:11 
分清楚real numbers 同natural numbers先啦!
Sorry for the late reply as the busy holiday routine caught up with me and prevented me from sitting quietly in front of the PC.
I'm puzzled why you have the idea why I've mixed up real numbers with natural numbers even though I had made reference to the number line.
Maybe you're referring to the first part of my statement "Mankind has been using real numbers since day one, but the concept of real numbers was not known to us until after the great Pythagoras." Actually it was not made up by me. Some scientists suggest real numbers are psychologically more primitive than natural numbers. The special role of natural numbers in the history of arithmetic has more with the discrete character of human language. if you are interested in such academic trivia, you can google for more information. My point is that primary school kids use fractions but it does not mean they know what real numbers mean, a mistake in logic kenwong888 made.
My table can take care of integers, fractional, irrational numbers (again a kid may not need to know this) depending on what numbers you get for the perimeter.
Mind you it is kenwong888 who first thought fit to use differentiation to tackle a primary school problem and later thought complete the square method also made do and suggested my method was not rigorous enough fot failing to consider real number solutions.
You can also find my following reply to 王家爸爸 useful.
Dear 王家爸爸
You're right about Europeans but...
There are many myths in mathematics, just like in many other things. It is only a myth that zero is a relative new toy for the humans. It's just that the zero symbol as we use today is relatively new but zero as a symbol (placeholder) was already used by the Babylonians and later by the Indians around 200 BC and the Chinese (孫髀算經, rather for the lack of a symbol). Zero as a number was first used in the sixth century AD by the Indians (It is the clever Indians who actually invented the Arabic numbers we use today, another myth in mathematics).
As to negative numbers, it was a new toy for Europeans but it appeared long before in China (孫髀算經 again, red for positive n black for negative) and in India.
My reference to Pythagoras is that only after Pythagoras irrational numbers started to be studied seriously and not just used as the Chinese did with 勾三股四弦五.
The mankind as a whole knew about the negative numbers and irrational numbers long long ago.
作者: lamyeelok 時間: 15-2-23 11:50
提示: 作者被禁止或刪除 內容自動屏蔽
作者: laorenjia 時間: 15-2-23 15:36
本帖最後由 laorenjia 於 15-2-23 15:37 編輯
lamyeelok 發表於 15-2-23 11:50 
毫無疑問人類對數字有概念一定始於"Natural Number"而不是"Real Number”,所以才命名為“Natural" 。其實又何需google找支持論據,試想想大家教導幼兒理解數字概念時,你估解釋何謂natural number容易啲定real number容易啲?
Natural numbers are called as such as they come naturally when we humans count things. No one can argue real numbers are much more sophisticated and more difficult to understand. However it doesn't contradict the proposition real numbers are used by humans even before we had language. Note I used the word "used" here and in the previous posts. Scientists even go as far as saying real numbers are used by animals like pigeons and rats. Again I encourage you to google for more information on this area if you're interested. I value more an academic curiosity in adults than in kids.
作者: lamyeelok 時間: 15-2-23 16:19
提示: 作者被禁止或刪除 內容自動屏蔽
作者: laorenjia 時間: 15-2-23 21:54
本帖最後由 laorenjia 於 15-2-24 01:46 編輯
lamyeelok 發表於 15-2-23 16:19 
以我的學識及見識根本無需如你般吓吓要靠google揾料支持論點,網上的確很多資訊,但最重要是要明白、理解、 ...
My dear learned friend lamyeekok
You seem to have the habit of assuming a lot of things.
First you assumed I had mixed up real numbers and counting numbers and now you assume I have no idea what "used" means. I know for sure your assumptions were both wrong. The only assumption that could well be true is that you're a more learned man than me, a laorenjia who often has troubles in understanding what learned people say. I really do not understand what you mean by "直至mankind有智慧地懂得real numbers之概念,那才是有意義。你估人類懂得natural number之概念先還是real number先呢?" I thought I made it quite clear humans mastered the concept of real numbers very late but we had been happily using our knowledge on integers, rational numbers and irrational numbers (all the components of a real number) all the time before Newton defined it for us. And you're saying this is meaningless? Why? I beg you to suppress your intuition and read the article "The cultural and evolutionary history of the real numbers" by Gallistel, Gelman and Cordes of UCLA and see what they say first.
Finally, the way you write, both Chinese and English, reminds me of one of our dear friends here. I even thought I was talking to him.
作者: eviepa 時間: 15-2-23 22:04
正如laorenjia所講,我地有個老朋友,有兩個modes,一個正常mode,好有見地;另一個係鬥爭mode,有時有道理,有時強詞奪理,目標只係鬥爭。
作者: compsognathus 時間: 15-2-23 22:50
本帖最後由 compsognathus 於 15-2-23 22:57 編輯
I myself believe that the mathematical concept of ratios had developed in humans long before natural or real numbers.
Many tribal cultures do not have many words for the natural numbers. For example, the Munduruku people only have words for one up until five. Studies done with Munduruku people show that they place numbers on the number line in a compressed, logarithmic form, so that the graph of their perceived distance between consecutive numbers resembles the graph of a logarithmic function. To a Munduruku, five dots is five times as great as one dot, but they notice that ten dots is twice as big as five dots, leading to this logarithmic graph.
A similar study performed using young children show that those without formal mathematics education mapped numbers identically to the manner in which Munduruku do so. As the child is introduced to the natural numbers and arithmetic, the curve slowly progresses into a straight line, the answer an educated adult would be most likely to give, provided the numbers were small. Even as adults, humans tend towards a logarithmic distribution of numbers, especially with larger numbers. For example, the terms “millionaire” and “billionaire” are thrown around almost as synonyms. When a similar study was carried out with adults, the adults showed logarithmic mapping when provided with amounts of dots too large to count quickly.
This concluded that humans have a predisposition to ratios rather than enumeration of individual numbers.
This is a rather logical deduction, as in the wild, circumstances would call for the application of ratios and proportions, not counting. When a tribal human sees two trees with fruit on them, he has to quickly deduce which of the trees bears more fruit. He does not need to individually enumerate the amount of fruit. When an enemy tribe is attacking the tribe of said human, he needs to be quickly able to deduce which of the tribes has more people, and therefore whether it is worth it to stand ground and fight or simply flee and avoid catastrophic losses. The ability to calculate ratios (though not necessarily express them in written form) is a survival skill in nature.
Another study involved a number of lionesses and a recording. One lioness was passing bushes, when a recording of one lioness roaring was played. The lioness stopped, looked around and moved on. When five lionesses passed by, three roars were played. The five lionesses roared in response and made an attack. This indicates that lions also have a concept of ratios, as they seem to recognize that a one-on- one fight was not worth it, but in greater numbers, they would readily fight.
To quote Stanislas Dehaene, "It appears that we, as humans, can access two different methods of numerical mapping. The logarithmic, ratio-based method is the most intuitive; we inherit it from our primate evolution and we still access it in the absence of precise mathematical tools. Through education, we also acquire a linear mapping. However, this does appear to be a cultural construct."
Sources:
1: Alex’s Adventures in Numberland (Alex Bellos)
2: http://www.sciencedaily.com/releases/2008/05/080529141344.htm (Source: Harvard University)
作者: BandC 時間: 15-2-23 23:01 標題: 引用:+本帖最後由+laorenjia+於+15-2-17+16:10+
原帖由 laorenjia 於 15-02-17 發表
本帖最後由 laorenjia 於 15-2-17 16:10 編輯
妻子話我頭腦簡單,channel 同細路仔差唔多,若我講數細路 ...
Laorenjia, 看了很多你的舊帖,學了很多,謝謝你!對於難溝通的人,不用太上心,希望你繼續教教我地呢d新手媽媽

作者: BandC 時間: 15-2-23 23:08 標題: 引用:正如laorenjia所講,我地有個老朋友,有兩
原帖由 eviepa 於 15-02-23 發表
正如laorenjia所講,我地有個老朋友,有兩個modes,一個正常mode,好有見地;另一個係鬥爭mode,有時有道理 ...


作者: lamyeelok 時間: 15-2-24 16:41
提示: 作者被禁止或刪除 內容自動屏蔽
作者: eviepa 時間: 15-2-24 17:07
越睇越似老朋友嘅鬥爭mode。
作者: hkpapa852 時間: 15-2-24 17:30
小應該用D簡單D既方法, 總長32, 要可以用"平方尺"嚟計:
1. 應該只可以係四方形或者正方形
2. 不論係四方形或者正方形, 應該可只兩等份, 所以32既一半, 即係16就係長和濶既總和
3. 以16分為兩個數字, A和B, 計算A*B組合最大既一個, A,B為16既組合有:
1,15 (15 sq feet)
2,14 (28 sq feet)
3,13 (39 sq feet)
4,12 (48 sq feet)
5,11 (55 sq feet)
6,10 (60 sq feet)
7,9 (63 sq feet)
8,8 (64 sq feet)
作者: laorenjia 時間: 15-2-24 17:48
回覆 lamyeelok 的帖子
Not interested to continue, sorry.
作者: laorenjia 時間: 15-2-24 17:53
BandC 發表於 15-2-23 23:01 
原來我都係頭腦簡單的人,哈哈!
Laorenjia, 看了很多你的舊帖,學了很多,謝謝你!對於難溝通的人,不用太 ...
I value a good opponent and I do miss the discussion with Wicked in the following old post which I'm not sure if you have read as well.
http://www.edu-kingdom.com/forum.php?mod=viewthread&tid=2270580&extra=&page=1
作者: kenwong888 時間: 15-2-24 18:21
lamyeelok 發表於 15-2-24 16:41 
不是我“assuming a lot of things”,而是你的理解力有限,係 assuming 我 "assuming a lot of things"而 ...
作者: lamyeelok 時間: 15-2-24 21:00
提示: 作者被禁止或刪除 內容自動屏蔽
作者: laorenjia 時間: 15-2-25 17:33
本帖最後由 laorenjia 於 15-2-25 18:00 編輯
琴日—家去睇戲,賀歲片中除港產片外,就只剩慌失失企鵝未睇,因家人受我影響,都喜歡睇戲。其它戲都睇過,張就時間就連粵語版都殺啦。全場我哋係唯一成人組別,好多細路,妻子隔離嗰個得兩歲左右。企鵝彈吓彈吓佢就笑,企鵝跌出飛機佢就喊,但我都唔係好得幾多,老婆係咁叫我咪笑得咁大聲。我個人就係咁,掂吓啲細路仔嘢就會turn into the child mode. 為咗教女兒數學,我確費了一番苦心,硏究用算術方法而非代數方法教女兒高小算術。但不知為什麼,有些家長總覺得我的方法不正統,非要用代數方法甚至微積分不可。這些家長要嗎是沒有孩子,要嗎孩子都不用教。可惜我接觸的孩子小學時都沒有好奇心學—元二次方程或者微積分。我只能嘆一句,這些家長都離開小學日子太遠了,都已經忘了自己小學數學的日子是怎樣走過來的。說來奇怪,我幾年前對Judy的雞兔同籠問題提出非代數的將兔仔腳斬去的血腥算術解法也有些家長與這裏的家長差不多,在提不出他們所謂正確的算術解法的同時,老是用'right?','understand?'等empty-worded questions and condescending tone 同人講嘢。幾年過去,如出—轍。
http://www.edu-kingdom.com/forum ... 75529&extra=&page=2
由post no. 29 開始。
As I said then,
Non-algebraic methods tend to more tedious than using equations but they tend to be more interesting as well.
It is always nice for a kid to master more advanced mathematical tools than those currently taught at school, but in no way this should be the requirement for all the students.
For example, in Mathematics at HKCE level, we are not supposed to use differentiation to find the minimum or maximum value of a quadratic function. The more tedious "completing the square" method is expected. Even in Additional Mathematics, to find the area of a triangle in coordinate geometry, one is not expected to use the more general, and much simpler "determinant" method learned in more advanced maths.
作者: kenwong888 時間: 15-2-25 20:52
laorenjia 發表於 15-2-25 17:33 
琴日—家去睇戲,賀歲片中除港產片外,就只剩慌失失企鵝未睇,因家人受我影響,都喜歡睇戲。其它戲都睇過, ...
HKCE???
Now is HKDSE!!!
Need to learn differentiation right???
作者: laorenjia 時間: 15-2-25 22:07
本帖最後由 laorenjia 於 15-2-25 22:31 編輯
kenwong888 發表於 15-2-25 20:52 
Are you still dreaming???
HKCE???
Now is HKDSE!!!
My dear friend
The guy dreaming definitely is not me. Pls read carefully. I was referringa to a post entry I wrote in 2007 when hkdse was nowhere close. And the last time I checked, core maths in hkdse still doesn't cover differentiation. RIGHT??? Finally pay attention to the main message other people are trying to convey, will you? RIGHT???
作者: eviepa 時間: 15-2-25 22:23
laorenjia 發表於 15-2-25 17:33 
琴日—家去睇戲,賀歲片中除港產片外,就只剩慌失失企鵝未睇,因家人受我影響,都喜歡睇戲。其它戲都睇過, ...
和你有點相似,我比較容易變成child mode,十年前對著年幼的女兒,可以聊天聊得大家都很高興,所以有時讓太太說我大唔透。不過,我正經起來,講家事國事天下事,太太卻搭不上咀來。自我陶醉一下,這可能叫做未失赤子之心。
我比較懶,懂得一種甚麼都能解的方法就不去理會低層次的方法。見你這幾個回合,我還很清楚記得當年你也是這樣,正想說你當年又是這樣,還未說出口,你自己就將當年的討論的論題列了出來。
講到長方形,相同邊界,長和闊甚麼比例面積會最大這問題,我在大概小五時,自己就想出了答案,肯定是正方形是面積最大。後來,六年級末段時學習座標的曲線,當中有例子介紹這問題,才知道長和闊不同比例可的形成一條曲線,亦證實了我的想法。
對高中孩子來說,明白正方形是面積最大,相信不難。
作者: kenwong888 時間: 15-2-25 22:32
laorenjia 發表於 15-2-25 22:07 
My dear friend
The guy dreaming definitely is not me. Pls read carefully. I was referring a post e ...
Still sleeping & dreaming right???
作者: laorenjia 時間: 15-2-25 22:54
kenwong888 發表於 15-2-25 22:32 
Both Module 1 & 2 include Calculus!!!
Still sleeping & dreaming right???
Dear dreaming friend
IT'S EXACTLY RIGHT!!!
M1 n M2 are called extended modules n are separate from so called Maths, RIGHT???
作者: laorenjia 時間: 15-2-25 23:05
本帖最後由 laorenjia 於 15-2-26 00:10 編輯
eviepa 發表於 15-2-25 22:23 
laorenjia,
和你有點相似,我比較容易變成child mode,十年前對著年幼的女兒,可以聊天聊得大家都很高興, ...
I actually feel pity for myself as if I am repeating part of my life, even possibly with the same people. And I saw the disappearance of some old friends like Wunma indicated by deleted entries in the old post and possibly judy. I feel agitated n sad suddenly. I never used punctuation marks like I just did, not even with wisekiddad n it was with an unworthy opponent(I'm a snob after all as Wicked described in the old post). I pity myself.
作者: eviepa 時間: 15-2-25 23:51
laorenjia,
wunma的消失,也令我有點悵然。BK再不是從前地踎茶餐廳,而是一間有規模的連鎖飲食集團,甚麼都變了。
女兒長大了,現在其中一個身份是補習老師,大學同學們也多有一份或以上補習的,有時也會傾談一下怎樣補習。談及補習英文,同學們都著重補文法;她則主力鼓勵閱讀。
很有趣,在第一代閱讀派開風氣之先,再經過第二代自創或跟隨者的分享後,現在《小學雜談》內,閱讀功效最大已近乎共識,文法練習已淪為輔助工具。
更加有趣的是,過去十年內,傾談過英語學習的老師中,用很大力氣去誘導子女英語閱讀的,比例十分高,尤其是英文老師。
第一代及第二閱讀派取得的成果有目共睹,經常上EK小學、中學論壇的,都知道甚麼是最好,但離開EK的,文法才是正宗。
英語老師用很大的力度讓自己的孩子閱讀,但自己的學生、別人的孩子,絕大部分卻仍懵然不知................。
我很有興趣繼續看下去,這格局幾時會變。
四十年前,狠狠地打仔被認為是教仔良方。現在絕少人抱這種態度。不打少罵肯定是香港教仔要走的路向,這格局幾時會變?
巨輪始終會轉向,我卻很喜歡用自己的螳臂,企圖加速巨輪的轉變。
作者: friendlyguy 時間: 15-2-26 01:25
There are different branches of mathematics. The method Uncleedward used in solving the chicken and rabbit problem is arithmetic which may be the most basic and fundamental category of mathematics. Simultaneous Equations is an algebraic method which, in my opinion can only be understood by student who has learned the basic arithmetic. That’s why, in my date, we learn to solve this problem arithmetically in P5 or P6. Once we learn algebra in secondary school, everybody will tackle this type of problem with simultaneous equations which is an easier and faster method. I don’t think any of these methods lacking proper mathematical treatment or insight into mathematical problems.
Knowledge has to be built up bit by bit.
Come back to the maths problem in this thread. The table made by laorenjia is using the `guess and check’ method which is considered a very proper way of tackling maths problem in primary school. A junior secondary student will solve it by completing the square (algebra) while a senior student will use differentiation (calculus). These are all proper maths methods.
I can’t image a student, even for the maths genius, can learn calculus without learning algebra and arithmetic first.
作者: kenwong888 時間: 15-2-26 07:17
本帖最後由 kenwong888 於 15-2-26 07:17 編輯
friendlyguy 發表於 15-2-26 01:25 
There are different branches of mathematics. The method Uncleedward used in solving the chicken and ...
Maybe the question should be revised as the fence is one-meter long each right???
Otherwise I only see the question ill-formed for primary student standard...
作者: friendlyguy 時間: 15-2-26 12:31
本帖最後由 friendlyguy 於 15-2-26 12:36 編輯
回覆 kenwong888 的帖子
I don't think it is necessary if the student already know fraction and decimal. If the data provided in the original problem is 30 ft. A student can still use guess and check method to deduce the answer should be 7.5ft.
6X9=54
7X8=56
8X7=56
9X6=54
Therefore:
7.5X7.5=56.25
However, if the student has not been taught with fraction, your condition will be necessary.
I believe the thread owner's son is a P5 student in SIS. I think fraction has already been taught.
Guess and check method is a very good exercise for primary student since require the student to manipulate a series of simple arithmetic equation before an answer come out. It can develop their mathematical sense for higher level maths., such as mathematical induction. In this case, a reasonably intelligent student can deduced that for a given perimeter, the area of a square is larger than a rectangle.
作者: eviepa 時間: 15-2-26 14:38
我肯定讀小五時我做到正確答案。如果小學五年班有多D呢類咁有挑戰性嘅題目,我就唔會覺得數學係一科悶蛋科目。
作者: laorenjia 時間: 15-2-26 21:08
本帖最後由 laorenjia 於 15-2-26 21:10 編輯
friendlyguy 發表於 15-2-26 01:25 
There are different branches of mathematics. The method Uncleedward used in solving the chicken and ...
Dear Friendlyguy
Thank you for coming to my rescue and your endorsement, again. It's interesting to note from your reply that you could be even older than me as I was not taught simultaneous equationso to solve chickens and rabbits questions in my primary school days. We just used simple equations. By letting the number of chickens be x, the number of rabbits is then 12(total number of chickens and rabbits) - x, we can then formulate the equation to account for the number of feet : x*2 + (12-x)*4=32. It's true though most secondary school students, once they have learned simultaneous equations, they tend to forget simple equations. However these questions seldom appear in primary schools today, with a few exceptions like the primary section of spcc.
Thanks again for your explanation.
作者: friendlyguy 時間: 15-2-26 23:03
本帖最後由 friendlyguy 於 15-2-26 23:05 編輯
回覆 laorenjia 的帖子
Dear Laorenjia,
The following is how we solve the chicken and rabbit problem in primary:
Assuming all animals has 2 legs. There will only be 12X2=24legs
But,there are 32 legs. Therefore, there is 32-24=8legs in surplus
These 8 legs are all come from rabbit. Each rabbit contributes 2 legs. Therefore, there is 8/2=4 rabbits
Putting all together: (32-12X2)/2=4 rabbits. There is 12-4=8 chickens
In my primary school days, X should not appear in the equation. No algebra of any form was taught.
friendlyguy
作者: laorenjia 時間: 15-2-27 12:08
本帖最後由 laorenjia 於 15-2-27 15:12 編輯
friendlyguy 發表於 15-2-26 23:03 
回覆 laorenjia 的帖子
Dear Laorenjia, The following is how we solve the chicken and rabbit problem ...
Then you must be younger than me. I was taught your arithmetic method as well at p5. Actually I used the same method In my old post but I just used cutting rabbits' feet to make it more interesting for kids to remember.
作者: eviepa 時間: 15-2-27 21:03
今次版主又做得好快手喎,我正想正式警告大家聰明仔爸又番黎,都未出手,聰明仔爸呢個新網名lamyeelok已經俾版主封左戶。
作者: laorenjia 時間: 15-2-28 11:47
eviepa 發表於 15-2-25 22:23 
laorenjia,
和你有點相似,我比較容易變成child mode,十年前對著年幼的女兒,可以聊天聊得大家都很高興, ...
我哋確實有好多地方似,有時睇你啲嘢,分分鐘以為喺自己寫嘅。
作者: laorenjia 時間: 15-2-28 17:43
回覆 laorenjia 的帖子
Eviepa
我諗你打漏咗個「認」字。
| 歡迎光臨 教育王國 (/) |
Powered by Discuz! X1.5 |






